Two-dimensional Arrays Can Be Thought of as Containing ________.

Blazon of data structure

In computer scientific discipline, an assortment information structure, or but an array, is a data construction consisting of a collection of elements (values or variables), each identified past at to the lowest degree 1 assortment index or fundamental. An array is stored such that the position of each element can exist computed from its index tuple by a mathematical formula.^{[1] [two] [3]} The simplest type of information structure is a linear array, also called ane-dimensional assortment.

For example, an array of 10 32-bit (4-byte) integer variables, with indices 0 through 9, may be stored as 10 words at memory addresses 2000, 2004, 2008, ..., 2036, (in hexadecimal: 0x7D0, 0x7D4, 0x7D8, ..., 0x7F4) then that the element with index i has the address 2000 + (i × 4).^[4]

The memory accost of the first element of an array is called offset address, foundation address, or base address.

Because the mathematical concept of a matrix can exist represented as a two-dimensional grid, 2-dimensional arrays are also sometimes called matrices. In some cases the term "vector" is used in computing to refer to an array, although tuples rather than vectors are the more mathematically correct equivalent. Tables are often implemented in the grade of arrays, peculiarly lookup tables; the word table is sometimes used every bit a synonym of array.

Arrays are amid the oldest and most important data structures, and are used by almost every program. They are also used to implement many other data structures, such as lists and strings. They effectively exploit the addressing logic of computers. In virtually modern computers and many external storage devices, the memory is a ane-dimensional array of words, whose indices are their addresses. Processors, especially vector processors, are ofttimes optimized for array operations.

Arrays are useful mostly because the element indices can be computed at run fourth dimension. Among other things, this feature allows a single iterative statement to process arbitrarily many elements of an array. For that reason, the elements of an array data structure are required to take the aforementioned size and should use the aforementioned data representation. The set up of valid alphabetize tuples and the addresses of the elements (and hence the element addressing formula) are commonly,^{[3] [five]} but non always,^[two] fixed while the array is in use.

The term array is often used to mean assortment information type, a kind of data type provided by most loftier-level programming languages that consists of a collection of values or variables that can be selected by 1 or more indices computed at run-time. Array types are often implemented by array structures; however, in some languages they may be implemented past hash tables, linked lists, search trees, or other data structures.

The term is also used, especially in the clarification of algorithms, to mean associative array or "abstract array", a theoretical figurer science model (an abstract data type or ADT) intended to capture the essential properties of arrays.

History [edit]

The first digital computers used machine-language programming to set upward and admission array structures for data tables, vector and matrix computations, and for many other purposes. John von Neumann wrote the kickoff array-sorting program (merge sort) in 1945, during the building of the first stored-program computer.^{[half dozen] p. 159} Array indexing was originally done by cocky-modifying code, and afterwards using index registers and indirect addressing. Some mainframes designed in the 1960s, such as the Burroughs B5000 and its successors, used memory segmentation to perform alphabetize-bounds checking in hardware.^[7]

Assembly languages more often than not have no special back up for arrays, other than what the auto itself provides. The earliest high-level programming languages, including FORTRAN (1957), Lisp (1958), COBOL (1960), and ALGOL 60 (1960), had back up for multi-dimensional arrays, and so has C (1972). In C++ (1983), class templates be for multi-dimensional arrays whose dimension is fixed at runtime^{[3] [5]} also as for runtime-flexible arrays.^[ii]

Applications [edit]

Arrays are used to implement mathematical vectors and matrices, as well as other kinds of rectangular tables. Many databases, small and large, consist of (or include) ane-dimensional arrays whose elements are records.

Arrays are used to implement other data structures, such every bit lists, heaps, hash tables, deques, queues, stacks, strings, and VLists. Array-based implementations of other data structures are frequently unproblematic and space-efficient (implicit information structures), requiring little space overhead, merely may take poor space complexity, particularly when modified, compared to tree-based data structures (compare a sorted array to a search tree).

I or more big arrays are sometimes used to emulate in-plan dynamic memory resource allotment, particularly memory pool allocation. Historically, this has sometimes been the merely manner to allocate "dynamic memory" portably.

Arrays tin be used to decide fractional or complete control flow in programs, equally a compact culling to (otherwise repetitive) multiple IF statements. They are known in this context as control tables and are used in conjunction with a purpose built interpreter whose control flow is altered according to values contained in the array. The assortment may contain subroutine pointers (or relative subroutine numbers that can be acted upon past SWITCH statements) that direct the path of the execution.

Chemical element identifier and addressing formulas [edit]

When data objects are stored in an array, individual objects are selected by an index that is unremarkably a not-negative scalar integer. Indexes are as well called subscripts. An index maps the array value to a stored object.

There are three ways in which the elements of an array can be indexed:

0 (zero-based indexing)

The first element of the assortment is indexed past subscript of 0.^[8]

1 (one-based indexing)

The first element of the array is indexed past subscript of one.

n (n-based indexing)

The base of operations index of an array can be freely called. Usually programming languages allowing n-based indexing besides permit negative index values and other scalar data types like enumerations, or characters may be used equally an assortment index.

Using zero based indexing is the design selection of many influential programming languages, including C, Java and Lisp. This leads to simpler implementation where the subscript refers to an offset from the starting position of an array, so the first element has an offset of zero.

Arrays can have multiple dimensions, thus it is not uncommon to admission an array using multiple indices. For case, a ii-dimensional array A with three rows and four columns might provide access to the chemical element at the 2nd row and 4th column by the expression A[one][3] in the instance of a naught-based indexing system. Thus two indices are used for a two-dimensional array, three for a three-dimensional array, and n for an north-dimensional array.

The number of indices needed to specify an element is chosen the dimension, dimensionality, or rank of the array.

In standard arrays, each index is restricted to a sure range of sequent integers (or consecutive values of some enumerated type), and the address of an chemical element is computed by a "linear" formula on the indices.

I-dimensional arrays [edit]

A one-dimensional array (or single dimension array) is a type of linear assortment. Accessing its elements involves a single subscript which can either represent a row or column index.

As an example consider the C announcement int anArrayName[10]; which declares a one-dimensional array of 10 integers. Here, the array can shop ten elements of type int . This assortment has indices starting from zero through nine. For example, the expressions anArrayName[0] and anArrayName[nine] are the first and terminal elements respectively.

For a vector with linear addressing, the element with index i is located at the address B + c × i , where B is a fixed base address and c a fixed abiding, sometimes called the address increment or step.

If the valid element indices begin at 0, the constant B is merely the address of the first element of the assortment. For this reason, the C programming language specifies that array indices always begin at 0; and many programmers will telephone call that element "zeroth" rather than "first".

Nevertheless, one can choose the index of the showtime chemical element by an appropriate selection of the base address B. For example, if the array has five elements, indexed 1 through v, and the base address B is replaced past B + 30c , and then the indices of those aforementioned elements will exist 31 to 35. If the numbering does non start at 0, the constant B may not be the address of whatsoever element.

Multidimensional arrays [edit]

For a multidimensional array, the chemical element with indices i,j would have address B + c · i + d · j, where the coefficients c and d are the row and column address increments, respectively.

More generally, in a m-dimensional array, the accost of an chemical element with indices i ₁, i ₂, ..., i _k is

B + c ₁ · i _i + c ₂ · i ₂ + … + c _thousand · i _g .

For example: int a[two][three];

This means that array a has 2 rows and iii columns, and the array is of integer blazon. Hither nosotros tin store vi elements they will be stored linearly but starting from first row linear then continuing with second row. The in a higher place array will exist stored as a₁₁, a₁₂, a_thirteen, a₂₁, a₂₂, a₂₃.

This formula requires merely yard multiplications and yard additions, for whatever array that can fit in memory. Moreover, if whatsoever coefficient is a fixed ability of 2, the multiplication can be replaced past bit shifting.

The coefficients c _k must exist chosen and then that every valid index tuple maps to the address of a distinct element.

If the minimum legal value for every index is 0, then B is the address of the chemical element whose indices are all naught. Equally in the one-dimensional case, the chemical element indices may be changed by changing the base address B. Thus, if a two-dimensional array has rows and columns indexed from ane to 10 and 1 to 20, respectively, then replacing B by B + c ₁ − 3c ₂ will cause them to exist renumbered from 0 through 9 and four through 23, respectively. Taking advantage of this feature, some languages (like FORTRAN 77) specify that array indices brainstorm at i, as in mathematical tradition while other languages (like Fortran 90, Pascal and Algol) let the user choose the minimum value for each alphabetize.

Dope vectors [edit]

The addressing formula is completely defined by the dimension d, the base of operations address B, and the increments c ₁, c ₂, ..., c _k . It is often useful to pack these parameters into a record called the assortment's descriptor or step vector or dope vector.^{[2] [3]} The size of each element, and the minimum and maximum values allowed for each alphabetize may also exist included in the dope vector. The dope vector is a complete handle for the array, and is a user-friendly way to laissez passer arrays as arguments to procedures. Many useful array slicing operations (such as selecting a sub-array, swapping indices, or reversing the direction of the indices) can exist performed very efficiently by manipulating the dope vector.^[2]

Compact layouts [edit]

Often the coefficients are called so that the elements occupy a contiguous area of memory. Nevertheless, that is non necessary. Even if arrays are always created with contiguous elements, some array slicing operations may create non-contiguous sub-arrays from them.

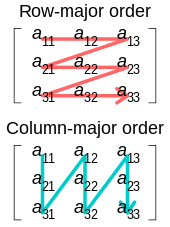
Illustration of row- and column-major lodge

There are two systematic meaty layouts for a two-dimensional array. For example, consider the matrix

${\displaystyle A={\begin{bmatrix}1&2&iii\\4&five&vi\\seven&viii&9\finish{bmatrix}}.}$

In the row-major order layout (adopted by C for statically declared arrays), the elements in each row are stored in consecutive positions and all of the elements of a row have a lower address than any of the elements of a sequent row:

1

two

3

4

5

vi

7

8

nine

In column-major lodge (traditionally used by Fortran), the elements in each column are consecutive in memory and all of the elements of a column have a lower address than whatsoever of the elements of a consecutive column:

i

iv

seven

2

v

8

three

6

9

For arrays with three or more indices, "row major society" puts in consecutive positions any 2 elements whose alphabetize tuples differ only by one in the last index. "Column major order" is analogous with respect to the commencement index.

In systems which utilize processor enshroud or virtual retention, scanning an array is much faster if successive elements are stored in consecutive positions in memory, rather than sparsely scattered. Many algorithms that utilize multidimensional arrays will scan them in a predictable society. A programmer (or a sophisticated compiler) may use this data to choose between row- or cavalcade-major layout for each assortment. For example, when calculating the product A·B of 2 matrices, it would exist best to have A stored in row-major order, and B in column-major order.

Resizing [edit]

Static arrays have a size that is fixed when they are created and consequently exercise non allow elements to exist inserted or removed. Still, past allocating a new array and copying the contents of the old assortment to it, it is possible to effectively implement a dynamic version of an assortment; see dynamic array. If this functioning is washed infrequently, insertions at the end of the array require only amortized constant time.

Some array data structures do not reallocate storage, merely do store a count of the number of elements of the array in use, chosen the count or size. This finer makes the array a dynamic array with a fixed maximum size or capacity; Pascal strings are examples of this.

Non-linear formulas [edit]

More than complicated (non-linear) formulas are occasionally used. For a compact two-dimensional triangular array, for instance, the addressing formula is a polynomial of caste ii.

Efficiency [edit]

Both store and select take (deterministic worst case) constant fourth dimension. Arrays take linear (O(n)) space in the number of elements n that they hold.

In an assortment with chemical element size grand and on a car with a cache line size of B bytes, iterating through an assortment of due north elements requires the minimum of ceiling(nk/B) enshroud misses, considering its elements occupy contiguous retentivity locations. This is roughly a factor of B/g amend than the number of cache misses needed to admission due north elements at random memory locations. As a consequence, sequential iteration over an array is noticeably faster in practice than iteration over many other data structures, a belongings called locality of reference (this does not mean however, that using a perfect hash or piffling hash inside the same (local) array, volition not be even faster - and doable in abiding time). Libraries provide low-level optimized facilities for copying ranges of memory (such as memcpy) which can be used to move contiguous blocks of array elements significantly faster than can be achieved through individual element access. The speedup of such optimized routines varies by array element size, compages, and implementation.

Retentiveness-wise, arrays are meaty data structures with no per-element overhead. There may be a per-assortment overhead (e.grand., to store alphabetize bounds) but this is language-dependent. It can also happen that elements stored in an array require less retentivity than the same elements stored in individual variables, because several array elements can be stored in a single word; such arrays are often called packed arrays. An farthermost (simply commonly used) example is the bit assortment, where every bit represents a single element. A single octet can thus hold upwardly to 256 unlike combinations of up to 8 unlike weather condition, in the most meaty form.

Array accesses with statically predictable admission patterns are a major source of data parallelism.

Comparison with other data structures [edit]

Comparison of list data structures

	Peek (index)	Mutate (insert or delete) at …			Backlog space, average
		Beginning	Terminate	Eye
Linked listing	Θ(n)	Θ(1)	Θ(1), known end chemical element; Θ(due north), unknown cease element	Peek fourth dimension + Θ(1)[9] [10]	Θ(n)
Array	Θ(1)	N/A	N/A	Due north/A	0
Dynamic assortment	Θ(one)	Θ(n)	Θ(i) amortized	Θ(n)	Θ(northward)[11]
Balanced tree	Θ(log n)	Θ(log n)	Θ(log north)	Θ(log n)	Θ(n)
Random-access list	Θ(log n)[12]	Θ(1)	N/A[12]	Due north/A[12]	Θ(due north)
Hashed array tree	Θ(1)	Θ(n)	Θ(1) amortized	Θ(n)	Θ(√n)

Dynamic arrays or growable arrays are similar to arrays but add the ability to insert and delete elements; calculation and deleting at the end is particularly efficient. Withal, they reserve linear (Θ(n)) additional storage, whereas arrays do not reserve additional storage.

Associative arrays provide a mechanism for array-like functionality without huge storage overheads when the alphabetize values are sparse. For example, an array that contains values only at indexes 1 and 2 billion may benefit from using such a structure. Specialized associative arrays with integer keys include Patricia tries, Judy arrays, and van Emde Boas trees.

Balanced trees crave O(log due north) time for indexed access, but also permit inserting or deleting elements in O(log due north) time,^[13] whereas growable arrays crave linear (Θ(n)) time to insert or delete elements at an arbitrary position.

Linked lists allow abiding time removal and insertion in the heart only have linear time for indexed access. Their retention use is typically worse than arrays, but is still linear.

An Iliffe vector is an culling to a multidimensional array structure. It uses a one-dimensional array of references to arrays of ane dimension less. For two dimensions, in detail, this culling construction would exist a vector of pointers to vectors, i for each row(pointer on c or c++). Thus an chemical element in row i and column j of an array A would exist accessed by double indexing (A[i][j] in typical note). This alternative structure allows jagged arrays, where each row may have a different size—or, in general, where the valid range of each index depends on the values of all preceding indices. It too saves i multiplication (by the column address increase) replacing it past a bit shift (to index the vector of row pointers) and i extra memory access (fetching the row address), which may exist worthwhile in some architectures.

Dimension [edit]

The dimension of an assortment is the number of indices needed to select an element. Thus, if the array is seen as a function on a set of possible alphabetize combinations, it is the dimension of the infinite of which its domain is a discrete subset. Thus a one-dimensional array is a list of information, a two-dimensional array is a rectangle of data,^[fourteen] a three-dimensional array a cake of data, etc.

This should not exist confused with the dimension of the set of all matrices with a given domain, that is, the number of elements in the array. For instance, an array with 5 rows and iv columns is 2-dimensional, but such matrices form a 20-dimensional space. Similarly, a 3-dimensional vector tin can exist represented by a i-dimensional array of size three.

See also [edit]

• Dynamic assortment
• Parallel array
• Variable-length array
• Bit array
• Assortment slicing
• Kickoff (computer science)
• Row- and column-major social club
• Footstep of an array

References [edit]

1. ^ Black, Paul Eastward. (13 November 2008). "assortment". Lexicon of Algorithms and Data Structures. National Establish of Standards and Technology. Retrieved 22 Baronial 2010.
2. ^ ^{a b c d e} Bjoern Andres; Ullrich Koethe; Thorben Kroeger; Hamprecht (2010). "Runtime-Flexible Multi-dimensional Arrays and Views for C++98 and C++0x". arXiv:1008.2909 [cs.DS].
3. ^ ^{a b c d} Garcia, Ronald; Lumsdaine, Andrew (2005). "MultiArray: a C++ library for generic programming with arrays". Software: Practice and Experience. 35 (ii): 159–188. doi:x.1002/spe.630. ISSN 0038-0644. S2CID 10890293.
4. ^ David R. Richardson (2002), The Book on Data Structures. iUniverse, 112 pages. ISBN 0-595-24039-9, ISBN 978-0-595-24039-5.
5. ^ ^{a b} Veldhuizen, Todd L. (Dec 1998). Arrays in Blitz++ (PDF). Calculating in Object-Oriented Parallel Environments. Lecture Notes in Calculator Scientific discipline. Vol. 1505. Springer Berlin Heidelberg. pp. 223–230. doi:x.1007/3-540-49372-7_24. ISBN978-3-540-65387-v. Archived from the original (PDF) on 9 November 2016.
6. ^ Donald Knuth, The Fine art of Calculator Programming, vol. iii. Addison-Wesley
7. ^ Levy, Henry Thousand. (1984), Capability-based Computer Systems, Digital Printing, p. 22, ISBN9780932376220 .
8. ^ "Array Code Examples - PHP Array Functions - PHP code". Reckoner Programming Web programming Tips. Archived from the original on 13 April 2011. Retrieved 8 April 2011. In nigh computer languages array alphabetize (counting) starts from 0, not from 1. Index of the get-go element of the array is 0, index of the second element of the array is 1, and so on. In array of names below yous can see indexes and values.
9. ^ Mean solar day 1 Keynote - Bjarne Stroustrup: C++11 Style at GoingNative 2012 on channel9.msdn.com from minute 45 or foil 44
10. ^ Number crunching: Why y'all should never, ever, E'er apply linked-listing in your code again at kjellkod.wordpress.com
11. ^ Brodnik, Andrej; Carlsson, Svante; Sedgewick, Robert; Munro, JI; Demaine, ED (1999), Resizable Arrays in Optimal Time and Space (Technical Report CS-99-09) (PDF), Section of Figurer Scientific discipline, University of Waterloo
12. ^ ^{a b c} Chris Okasaki (1995). "Purely Functional Random-Access Lists". Proceedings of the Seventh International Conference on Functional Programming Languages and Estimator Architecture: 86–95. doi:10.1145/224164.224187.
13. ^ "Counted B-Copse".
14. ^ "Two-Dimensional Arrays \ Processing.org". processing.org . Retrieved 1 May 2020.

External links [edit]

Look upward array in Wiktionary, the complimentary dictionary.

• Data Structures/Arrays at Wikibooks

hargroveauntithe.blogspot.com

Source: https://en.wikipedia.org/wiki/Array_data_structure

Share this post